Comments/Ratings for a Single Item
Thank you for confirming my assessment. I think that the variants should be made for people - and not for machines. It may well be that the individual feels challenged. But dealing with the matter ties up considerable resources; this puts other variants at a disadvantage! At least that's my opinion.
Let's see what y'all think of this (some cache flushing may be required):



I'm think I might also replace 0 and 5 with W and B, renaming 00 to WH (White Home) and 50 to BH (Black Home), also finding something else for A0 and 5A (which I think is needed anyway)
PS: This has also given me some ideas about how a practical playspace could be constructed!
PS: This has also given me some ideas about how a practical playspace could be constructed!
Here's a first-sketch look at what I was thinking:

Obviously I need to also include support struts, labels, and such; I probably also need to increase the vertical clearance, and it probably could benefit if I change the tray colors to black, white, and grey.
As it currently stands, with 1" squares it's 5'9" across and 5'4" wide. I may be able to reduce the former measurement with a little rearrangement (like changing the side Faces to a vertical relationship), but that's roughly the size I was expecting.
As I say, it's not impossible to do, and an interested party certainly could put one together. I'm not ruling out doing it myself, if only for a demo setup at C3 Game Con -- that, or another large 3D setup that I haven't posted yet... or maybe even both.
Let's see what y'all think of this (some cache flushing may be required):
The diagrams are not enough for me to understand it. I need a written description of the rationale behind it.
With it's own King help, 2 Rooks can force checkmate a lone King without a board's edge.
4D-Chess (4x4 array of 4x4 boards) had been investigated by Maack (famous for his 3D-Chess) in the early 20th c. Dawson wrote a paper about it in 1926.
Also V.R.Parton was much interested in this. Let's mention his Sphinkian Chess (3x3 array of 4x4 boards). And above this, his Ecila Chess in 1970 with a cubic 2x2x2 array of 2x2x2 cubes, a 6D-Chess.
 Joe Joyce wrote on Fri, Dec 8, 2023 09:40 AM UTC in reply to Jean-Louis Cazaux from 06:57 AM:
Joe Joyce wrote on Fri, Dec 8, 2023 09:40 AM UTC in reply to Jean-Louis Cazaux from 06:57 AM:Jean-Louis, is there an available copy of Maack's and/or Dawson's work? I didn't turn anything up from an online search.
Apologies, Bob, for dragging other designers' 4D games onto your page. But 4D variants are an interesting topic, with little available information, and both Ben R. and I are interested in 4D variants and we've each done at least one. Grin, I see that unlike me, you were not aiming for extreme playability.
The norm seems to be the 4x4x4x4 board. Dale Holmes did a 5x5x5x5 version and posted it in the wiki, but it no longer exists there. I found V.R. Parton's 4D Sphinx Chess to be surprisingly timid for him. The individual 2D 4x4 boards that make up most 4D boards are present, but in a 3x3 array, rather than 4x4. To me, individual 4x4 2D boards scream for a full 4x4 array, not Parton's setup. I originally felt that this was a lack of imagination, but lately I've been wondering if he did it deliberately for playability.
One problem I was concerned about was how chaotic a game could become in just a few moves. When a game has "infinite sliders" and short range leapers coupled with both a larger board and several additional ways to go when moving to an adjacent location, things can get quickly crazy, with pieces appearing almost randomly across the board. The knight has a move which translates perfectly to 4D. Allowing it to jump also makes it a killer piece, literally! Even forcing it to slide 2+1 or 1+2 without the leap still means the knight has 2 paths to its target square.
One major difference between this game and the more usual 4D variant is that it is played on the surface of a tesseract rather than through four dimensions. So, it is a 4D variant in the same sense that Spherical Chess is a 3D variant. Like Spherical Chess, the pieces have 2D movement, but the board has properties of a higher dimensional playing area.
Apologies, Bob, for dragging other designers' 4D games onto your page. But 4D variants are an interesting topic, with little available information, and both Ben R. and I are interested in 4D variants and we've each done at least one. Grin, I see that unlike me, you were not aiming for extreme playability.
No apologies necessary; it's a valid topic here.
The difference between this variant and other 4DVs is (as Fergus pointed out) that this one doesn't use 4D movement; it's the usual 2D movement, on the surface of the tesseract. That affects the playability to an extent, though as I've been arranging things I'm starting to see that it might actually be playable after all, if one doesn't mind using a 3D setup (which I think some 4D games do anyway).
Still, it's easier to lay out 256 squares for a 4x4x4x4 game than 504 squares (not counting the corners) for a 24x5x5 game, and that's not even considering the complex relationships of each side to its neighbors. I've tried to simplify the latter aspect, and I'm in the process of doing so further until it's easy enough for neurotypicals* to understand.
Even forcing it to slide 2+1 or 1+2 without the leap still means the knight has 2 paths to its target square.
If you change the move to [W-F] (one orthogonal followed by one diagonal) that would reduce it further.
*My apologies if that comes across as condescending.
The diagrams are not enough for me to understand it. I need a written description of the rationale behind it.
I've fully changed the graphics, and written out an explanation as well as I could, and also gotten a start on the physical board setup (this may become a Project later on).
A question on that, though: is 5" clearance between boards (with 1" squares) sufficient? I could increase it to 7.5". Too close makes it hard to reach the pieces in the middle, but too far makes it hard to see the relationships between pieces, which would already be a challenge even for me.
Also, would it be helpful to use a different tray color on the Home and Opposing Faces?
(Those trays, by the way, will also be labeled as to which Face they are and which Faces each side leads to.)
I've fully changed the graphics, and written out an explanation as well as I could
Your written description is inadequate, and your diagrams are too crowded to be helpful.
Your written description is inadequate, and your diagrams are too crowded to be helpful.
I have a vague idea about what to do about the latter; I'll get to work on the former this afternoon.
I have a busy afternoon today, so I got a start on things early. There's still some work to be done (including a reworking on a couple of the illos), but hopefully this is an improvement.
The rhomboid illos should help, at least with the four faces they focus on and their neighbors.
I'm willing to make similar illos for the four Open Faces, but I don't know if I want to make one for each of the remaining 16 (if it's truly needed, though, I will).
Addendum: And I'm guessing, since nobody's said anything, that 5" will be sufficient vertical clearance for the playspace.
@Joe Joyce: I will look into my many books and articles what my sources are. Right now I have "A Guide to Fairy Chess" from Anthony Dickins in hands where some details about 4D-chess by Maack and by Dawson are given and commented.
Of course, Pritchard has also listed Maack's: Maack’s Four-dimensional Chess (Ferdinand Maack, 1926 or earlier). Maack added an extra dimension to his game to create a board 4x4x4x4 which, whilst appealing to problemists, failed to recruit players. (Chess Amateur, December 1926)
@ Jean-Louis Cazaux:
Regarding Maack's 4D CV game, do you know if it looks strongly like my own first try at a 4D CV?:
https://www.chessvariants.com/rules/4chess-four-dimensional-chess
I've started putting the labels on the trays for the 3D setup. I've only done a few, to see how clear the information is.

Between this, plus the text and illos in the article, does it seem clear where things go and what's supposed to happen?
Between this, plus the text and illos in the article, does it seem clear where things go and what's supposed to happen?
No, a coordinate system is an address system, and it should provide addresses independently of what it provides addresses to. Suppose I told you that the White House was at WH Pennsylvania Ave. Would that help you find it? WH and BH are not helpful designations, because they do not indicate the relations of these areas to each other or to other areas of the board. Likewise, adding the letter A to some areas has not been helpful. By naming areas of the board after their function in the game, you have left their location obscured, and you have made it more difficult for the reader to understand how the geometry of a tesseract works.
I will send you a photograph of the relevant pages.
I can think of only two actual coordinate systems for this. One would be to number each of the eight cubes, and designate each face according to which two cubes it connects The other is to assign a binary notatioin, with White's Home Face as 0000 and Black's as 1111. The problem with either of those is that one would likely have to already understand four-dimensional geometry to understand it, and part of the goal here is to help the reader understand four-dimensional geometry. It's not as simple as when using the interior of the tesseract rather than its surface.
The system here starts with the two Faces where White and Black start, designates the four directions (1-4) that one can leave that board, and the two paths (A/B) that can be taken to reach the other side along with four faces (12, 23, 34, 14) that can be used to switch from one path to the other. Except for those last four, all Faces have a designation that describes its relationship to one of the Home Faces, and by implication the other as well. If the designation starts with 0, then you know it's adjacent to White's Home Face; if it starts with 5, then it's adjacent to Black's (I may decide to change those to W and B just to be fully clear). If it ends with A, then you know it's adjacent to AX; if it ends with B, then you know it's adjacent to BX. If its number is 2, then you know it's between 1 and 3; and so forth.
WH (White's Home) and BH (Black's Home) should clearly imply that they are on opposite ends. There are CVs on this site where Black and White don't set up on opposite ends of the board, but they're extremely rare (of the hundred or so that I've perused, I've seen maybe two). When one understands that, then it seems natural that WH is connected to all of the Faces that start with W, while BH is connected to all of the Faces that start with B. This diagram shows how 1, 2, 3, and 4 are arranged for White, and this one for black; I think they'll be even clearer if the sides are designated as W or B instead of 0 or 5. I could also change the middle digits to N/S/E/W; most English-speakers understand the relationships of those.
A and B are arbitrary, and can't be anything else; the only significant thing about either is that it isn't the other one. It's a little like having two hallways connecting two room together, with a door halfway down connecting them (that door representing the "grey" Faces). If I change all the numbers above to letters, then these will probably be called 1 and 2, or perhaps L and H for Low and High.
Edit: I think I will, in fact, make the alphanumeric changes I mention. It's a bit more intuitive.
I can think of only two actual coordinate systems for this. One would be to number each of the eight cubes, and designate each face according to which two cubes it connects The other is to assign a binary notatioin, with White's Home Face as 0000 and Black's as 1111.
I think you're forgetting the one I already described. You were able to tell from my description of it that it accurately represented the geometry of a tesseract. Additionally, I was able to describe it clearly without using any labeled diagrams. The only image it referenced was the 2D representation of a tesseract that looks like one cube inside of another with lines connecting their corners. It works like this:
- Initially number the inner and outer cubes like a die with 1 opposite 6, 2 opposite 5, and 3 opposite 4, using the same numbers for the same sides of each.
- Designate a face on the inner cube by preceding it with 0, which gives us 01, 02, 03, 04, 05, and 06.
- Designate a face on the outer cube by preceding its number with the same number, which gives us 11, 22, 33, 44, 55, and 66.
- Designate any face between the inner and outer cubes by the two numbers initially given to the inner and outer cube faces it lies between, writing the lower number first to avoid redundancy. This gives us 12, 13, 14, 15, 23, 24, 26, 35, 36, 45, 46, and 56.
I do recall that, but I find it rather generic. (I also found it confusing the first time around, though now reading it for the fourth time I now finally understand what it's supposed to look like.)
I'll try this more descriptive system that I've devised, setting the coordinates in relation to the Home Faces (I'm typing it out even now, interrupting that work only to write this Comment), and if that works at all, and if the file system lets me*, I'll make a diagram or three using your method, with explanation and a key to translate to/from mine.
*It should. I've been hitting file size limits, but I plan to crop and reduce all of it once I find something that actually works.
Thanks. I would think Maack naturally could have chosen the same 8 piece types I did for my first 4D CV attempt (i.e. including 3D Unicorns and 4D 'Balloons', or whatever he called the latter), though his 4D CV's setup just as easily could have been a different one than mine, and he may have had his pawns move/capture differently too.
@Kevin: I just sent a scan of the relevant pages to you
25 comments displayed
Permalink to the exact comments currently displayed.
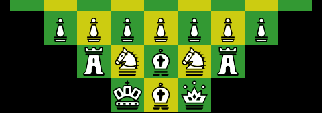
To expand a little on what I say in the text and early comments from Fergus and myself, this is probably not playable except on a computer (though discussions have shown me how it might be done as a live game). I'd certainly be willing to try it out as a computer-based game; but really, like Salmon P. Chess -- which partly inspired this -- and a few others, the goal is to illustrate more than to make an actual game, though in this case the latter is certainly possible.
I've seen computer simulations of four- and five-dimensional Rubik's cubes, and that was many years ago, so I know that programming this should be a breeze for someone with sufficient tools, experience, and dedication (of which I definitely lack the first two).
Most humans aren't capable of truly visualizing and understanding higher-dimensional constructs, so if this helps even one person with that, then I've achieved my goal.