Comments/Ratings for a Single Item

Bison moves h7-e6-g3-d4-c1-f2-c4 to force mate in six in this position: White King (b3), White Bison (h7), Black King (b1). The Black King has very little freedom - it must alternate between (b1) and an adjacent square. I could use an answer to the following question. In general, can the Bison force a lone King into a corner (and checkmate) on a 12x12 board? [EDIT] For a positive answer, check out some comments made in July 2008.

WHITE MATES IN SIX

The Bison definitely has mating potential on an 8x8 board. Denoting Bison by Y: I have built a tablebase for the KYK end-game, and it is 100% won for white to move. (With black to move there are of course positions where the bare King captures an undefended Bison on the first move, and these are then draw.) Longest mate against best defense takes 27 moves.

I cannot build tablebases on other boards yet, but I adapted Joker80 so it would move Knights like Bisons. If I let it think a few min/move it does find mate in 20 or so in all psositions where the bare King is not too well centralized (and the white King is). As it is rather easy to drive the bare K out of he center with K+Y, this makes it likely that KYK is also won on 10x8. If I give the winning side a time-odds handicap of a factor 100, (40/60 vs 40/0:36) so it searches only 9-12 ply, where the defending King searches 22-28 ply, the bare King starting from w:Ke1,Yg1 b:Ke8 gets menouevred into mated-in-31 position quite rapidly (without the K+Y side knowing yet), after which it sees the mating net being tightened until the winning side finally gets a mate-in-12 within its horizon.

I couldn't say anything about 12x12.

Note that the Bison is equivalent to the patented Falcon in these games, as there is not enough material on the board to block the Falcon moves.

On 2008-07-06 H. G. Muller concluded that King and Bison can force checkmate on boards as large as 12x12. I once thought about using Bisons, but later changed my mind. Back in February, 2000 Sergey Sirotkin used both Bisons and Camels in his 7x7 chess variant HERD.

'On 2008-07-06 H. G. Muller concluded that King and Bison can force checkmate on boards as large as 12x12. '

That was actually even 14x14. King + Bison vs Kings is absolutely won on 14x14 and smaller, with white to move. (i.e. not a single draw position.) The Bison cannot be trapped in a corner; its large stride simply makes it leap out of trouble. In addition there are no corner stalemates (such as in KNK:

 k N . . . .       ), because a Bison can alway check the square
 . . . . .            next to it in 1 move. 
 K . . . .
 . . . . 
 .

The longest mates (against perfect defense) are:

BOARD MOVES (K,Bi,k)
16x16: 76 (a4,b7,b1)   (but 90% of all wtm positions are draw) 
14x14: 82 (a1,n14,c3)  (100% won)
12x12: 55 (a1,L12,c3)      '
10x10: 40 (a1,j10,c3)      '
 8x8:  27 (a2,b2,b4)       '

H.G. Muller, 
This is not a bison question, but do you have a ubuntu version of Joker?, although it is apparently working under wine.

@HG: on the link to test the Bison for mates, I don't see the Bison on the diagram. Can this be corrected? Thanks

https://www.chessvariants.com/membergraphics/MSinteractive-diagrams/EGT.html?betza=CZ&name=Bison&img=wildebeest3

The "Try it!" link should work now; I clipped off the 3 from the requested image. I guess this error crept in when I changed the checkmating page to using alfaeriePNG, which does not have a wildebeest3. I don't really know which set has, though, as the old alfaerie gifs don't seem to have it too.

@HG: thanks, after cleaning the cache (of course), it works. Still, I don't see how a Bison+King can mate a lonely K.

Well, if you play with black the Applet should demonstrate it to you. The key is that the Bison has (say) to be on c4 with its King on b3 to checkmate on a1, and to force the bare King to step to a1 it had to attack c1 on the move before. So it has to move from c1 to c4 in two moves. (Actually a retrograde capture plus a normal non-capture, but since it is symmetric and non-divergent there is no need to distinguish the move types.) It can do that via f2 or f3, which means it must have to be on one of these in the mated-in-1 positions.

It could be that the King was forced to a1 earlier without the Bison being on f2 or f3, e.g. namely when the Bison is on any other square it could reach from c1 (so a4, b4, d4 or e4). The Bison then has two moves to reach f2/f3, as the next move Ka1-b1 is forced without the Bison's help. (And you could also play Kb3-c2 to move the mate to the other edge, and make d3 the target where the Bison could checkmate, after coming from b6/c6.) If you look at what a Bison can do in 2 moves, it is a lot. From any of its move targets to any other. That is W, D, H, WX, F, D, A, N, FX, NX, DY moves, amongst others. For the close-by targets there are only very few that it cannot reach in two moves. It particular, from f3 it could go to a4 (via d6), b4 (via e6), d4 (via g6) and e4 (via h6), so on all these squares it has mate in 3.

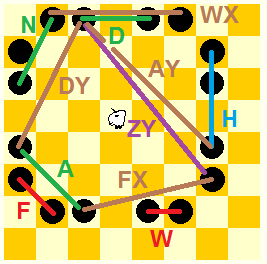
If a piece can make these final steps to force mate on a bare King that is in a corner, it can usually force mate from any position, if the board is not too large. What is too large is determined by how strong the piece is, and a Bison is pretty strong. (But it cannot force a King to the edge all by itself, such as a Centaur can, so at some size it will lose its mating potential.) For a piece with only large leaps, the board must also not be too small.

Thank you HG, this tool is very convenient

Over on the Piececlopedia: Gnu page, George Duke mentions that the Bison can return to its original square in five moves. The example below makes three Camel moves, followed by two Zebra moves. Strictly speaking, this is not triangulating (three moves).

d5-g6-h3-e4-b2-d5

Just like Waffle.