Check out Janggi (Korean Chess), our featured variant for December, 2024.

This page is written by the game's inventor, Florin Lupusoru.

Mathematichess

Mathematichess is a new chess variant created for both chess lovers and mathematicians. It is played on a normal chess board and involves unique rules that incorporate mathematical concepts.

This game is a combination of Chess, Go, Rummy, and Maths. The objective of the game is to control the empty squares that give value points to the owner. The value of a square depends on the number and type of pieces surrounding it.

Setup

The initial setup is an empty board.

Each player has 5 Kings, 5 Queens, 5 Rooks, 5 Bishops, 5 Knights,  and 5 Pawns, with values ranging from 10 to 1. 

The game has two stages:

  1. In the first stage players take turns placing their pieces anywhere on the board until all pieces are on the board.
  2. In the second stage players battle for controlling the empty squares. 

Each player has 30 pieces. When all pieces are on the board four empty squares should remain. The empty squares are the focus of the game. 

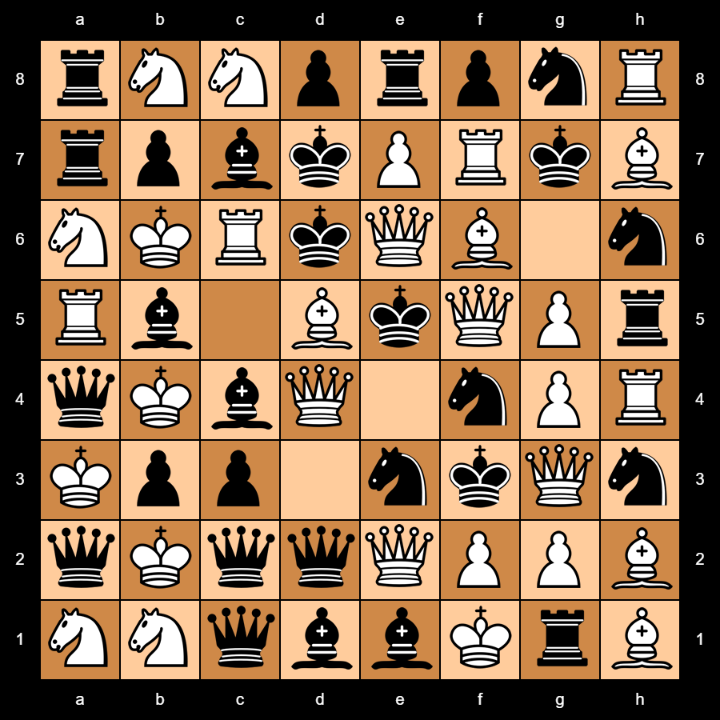
Here is an example diagram for the game.

Pieces

Each piece has a certain numerical value.

These values are relative the position of a piece on the chessboard. 

Pieces have to move differently from classical chess due to the crowded board.

All piece movements are only allowed towards an empty square.

 

Rules

There is no castling, no en passant, no promotions, no check, and no check mate. Also, there is no capturing of pieces. The battle is arround the empty squares. Each empty square represents a territory whose value is given by the value of the pieces (Settlers) around it. The objective of the game is to control as many territories as possible. 

Pieces surrounding a territory (one square away orthogonally or diagonally) are called Settlers. The value of a teritory is given by the value of its Settlers. 

Each teritory can have 8 Settlers in the centre of the board, 5 Settlers on a side, and 3 on a corner. Players are allowed to join territories (two or three, or more empty squares) if they can control them. 

The value of a territory is calculated as following:

Pieces controlling the sides of a territory (First Class Settlers) are more important than the pieces controlling its corners (Second Class Settlers). 

Kings and Queens represent the Royals. 

A game cannot end in the first stage. 

In the second stage players take turns moving one piece at the time around the empty squares, attempting to make as many points as possible.

If a player refuses to play a turn because, by doing so, he might lose points, his oponent is allowed to play one more move. 

If the same player refuses to play for the second time the game ends. 

The game also ends when a player has no more legal moves, or by agreement between the two players if a certain territory configuration has been reached. 

At the end of the game each player calculates the value of his own territories. 

Players may also decide the winning conditions and the value of the additional (bonus) points for different pieces combinations in their own territories.

If a player has at least 50% + 1 points in a territorry, he also takes away the points of his opponent.  

The quality and posittion of the Settlers is more important than the numerical advantage. 

Additional points are given to players with three or more Settlers of the same kind controlling a territory.

In this case, if a player has at least three Pawns, or Bishops, or Knights etc in the same territory, the bonus points will be calculated by adding the value of these pieces, and then their value gets tripled, and added to the overal value of that territory. This is only true for territories with eight Settlers.

For territories with five or three Settlers, bonus points are only given for at least three, or two settlers of the same kind respectively. 

If a territory is also entirely composed of pieces of the same color, the overall value of that territory will be doubled. 

If the points ratio between black vs white over a territory, regardless of the number of pieces, is 50:50, nobody will get the points. 

Here is an example diagram of white refusing to play because he will lose points.

White clearly wins in this example. 

Calculating the points:

1) The c5 territory

a) White = (10x2) + (3x2) + 10 = 36 points

b) Black = (3x2) +(3x2) +3 = 15 points

White wins = 36 + 15 = 51 points.

 

2) The d6 territory

a) White = (10x2) + (9x2) + (3x2) + 5 + 1 = 50 points

b) Black = (10x2) + 10 = 30 points.

White wins = 50 + 30 = 80 points.

 

3) The e3 territory

a) White = (9x2) + (9x2) + (9x2) + 1 = 55 points. 

b) Black = (10x2) + 10 + 9 + 4 = 43 points.

c) Bonus points

White gets additional bonus points because of the three Queens.

The three Queens bring 54 points 

This value gets tripled.

54 x 3 = 162 bonus points

White brings 55 + 162 = 217 points. 

We now add this with the black points.

217 + 43 = 260 points for white.

 

4) The h6 territory

a) White = (3x2) + (1x2) + 1 = 9 points

b) Black = (5x2) + 10 = 20 points

Black wins with 20 + 9 = 29 points. 

 

Result:

White wins with 391 points against 29 points for black.

 

Notes

The c5 and d6 territories are not connected even though they share some Settlers. 

Territories can only be connected orthogonally to count as a single territory. 

Players are free to decide themselves the value of the bonus points. 

The above calculation is just an example, not a rule. 

Players can also take inspiration from Poker and aim to create "Four of a Kind" or "Full House" combinations for their controlled territories, with additional bonus points for each variant. 


This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.

By Florin Lupusoru.

Last revised by Florin Lupusoru.


Web page created: 2023-05-07. Web page last updated: 2024-01-04

Revisions of MSmathematichess