Check out Janggi (Korean Chess), our featured variant for December, 2024.

This page is written by the game's inventor, Florin Lupusoru.

Mathematichess

Mathematichess is a new chess variant created for both chess lovers and mathematicians. It is played on a normal chess board and involves unique rules that incorporate mathematical concepts.

This game is a combination of Chess, Go, Rummy, and Maths. The objective of the game is to control the empty squares that give value points to the owner. The value of a square depends on the number and type of pieces surrounding it.

Setup

The initial setup is an empty board.

Each player has 5 Kings, 5 Queens, 5 Rooks, 5 Bishops, 5 Knights, and 5 Pawns, with values ranging from 10 to 1.

The game has two stages:

  1. In the first stage players take turns placing their pieces anywhere on the board until all pieces are on the board.
  2. In the second stage players battle for controlling the empty squares.

Each player has 30 pieces. When all pieces are on the board four empty squares should remain. The empty squares are the focus of the game.

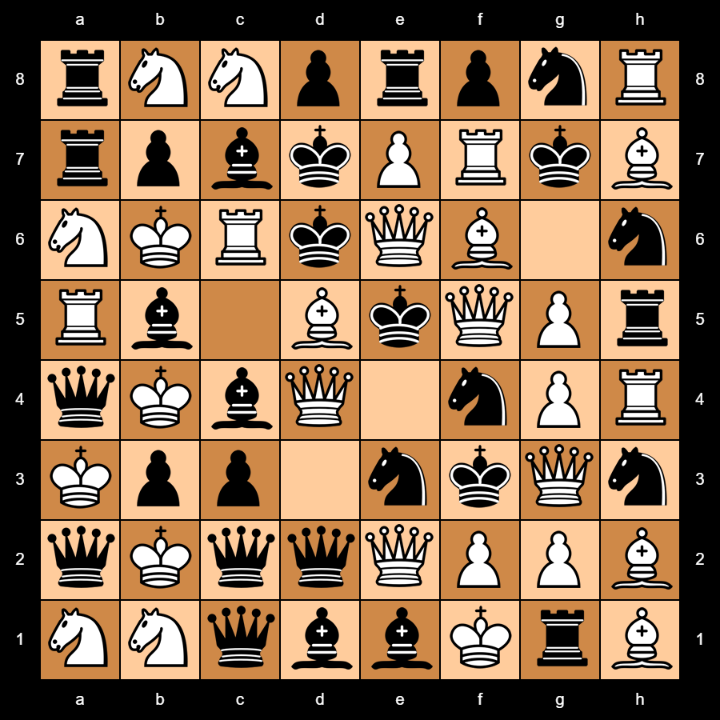
Here is an example diagram for the game.

Pieces

Each piece has a certain numerical value:

Pieces have to move differently from classical chess due to the crowded board.

All piece movements are only allowed towards an empty square.

Rules

General rules

There is no castling, no en passant, no promotions, no check, and no check mate. Also, there is no capturing of pieces. The battle is arround the empty squares. Each empty square represents a territory whose value is given by the value of the pieces (Settlers) around it. The objective of the game is to control a majority of territory points.

Each teritory in the center of the board can have 8 Settlers, territories on a side 5 Settlers, and a corner territory just 3 Settlers. Players are allowed to join territories (two or more empty squares) if they can control them; they must be orthogonally connected to count as a single territory.

A player may pass their turn. If a player passes two turns in a row, the game ends (so their opponent will have had the last move). The game also ends when a player has no more legal moves, or by agreement between the two players if a certain territory configuration has been reached.

In order to avoid repetition, players are not allowed to move the same piece twice in a row to the same squares. 

Territory valuation

Base value

The value of a territory is calculated as following:

The player contributing the majority of the points of a territory wins all the points of that territory. In case of equal contributions, the players split the points.

Bonus points

Additional points are given to players with multiple Settlers of the same kind controlling a territory. For a territory in the center or side of the board, the bonus requires at least three settlers of the same type (three pawns, or three bishops, etc.). For territories on a corner of the board, bonus points are given for having at least two settlers of the same kind. In either case, the bonus points are calculated by adding the value of these like pieces, and then their value gets tripled, and added to the overal value of that territory.

If a territory is also entirely composed of pieces of the same color, the overall value of that territory is doubled.

Example scoring

Here is an example diagram of white refusing to play because he will lose points. White clearly wins in this example.

1) The c5 territory

a) White = (10x2) + (3x2) + 10 = 36 points

b) Black = (3x2) +(3x2) +3 = 15 points

White wins = 36 + 15 = 51 points.

 

2) The d6 territory

a) White = (10x2) + (9x2) + (3x2) + 5 + 1 = 50 points

b) Black = (10x2) + 10 = 30 points.

White wins = 50 + 30 = 80 points.

 

3) The e3 territory

a) White = (9x2) + (9x2) + (9x2) + 1 = 55 points. 

b) Black = (10x2) + 10 + 9 + 4 = 43 points.

c) Bonus points

White gets additional bonus points because of the three Queens.

The three Queens bring 54 points 

This value gets tripled.

54 x 3 = 162 bonus points

White brings 55 + 162 = 217 points. 

We now add this with the black points.

217 + 43 = 260 points for white.

 

4) The h6 territory

a) White = (3x2) + (1x2) + 1 = 9 points

b) Black = (5x2) + 10 = 20 points

Black wins with 20 + 9 = 29 points. 

 

Result:

White wins with 391 points against 29 points for black.

 

Alternative ending

Supposing the black player has an extra move and he decides to use the King from e5 and push the Bishop from d5 to c5. 

We now have the following situation:

Recalculating the points:

1) The c5 territory moves to e5.

a) White = (9x2) + (9x2) + 3 = 39 points

b) Black = (10x2) + (4x2) + 10 + 4 = 42 points

Black wins with 42 + 39 = 81 points.

 

2) The d6 territory is recalculated.

a) White = (10x2) + (9x2) + 5 + 3 + 1 = 47 points

b) Black = (10x2) + (10x2) = 40 points

White wins with 47 + 40 = 87 points.

 

3) The e3 territory remains the same.

White wins with 260 points.

 

4) The h6 territory remains the same.

Black wins with 29 points.

 

Result

White = 260 + 87 = 347 points.

Black = 40 + 29 = 69 points. 

Notes

The quality and position of the Settlers is more important than the numerical advantage.

Players may also decide the winning conditions and the value of the additional (bonus) points for different pieces combinations in their own territories. For examples, taking inspiration from Poker, players may agree to create "Four of a Kind" or "Full House" combinations for their controlled territories, with additional bonus points for each variant. 


This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.

By Florin Lupusoru.

Last revised by Florin Lupusoru.


Web page created: 2023-05-07. Web page last updated: 2024-01-04

Revisions of MSmathematichess