Comments/Ratings for a Single Item
 H. G. Muller wrote on Thu, Sep 27, 2018 06:40 PM UTC:
H. G. Muller wrote on Thu, Sep 27, 2018 06:40 PM UTC:I don't understand your problem. I don't even see a 'middle square'; the middle of the board coincides with square corners. All squares seem reachable without jumping over any 'holes' in the board.
H.G. Miller, I'm sorry, I missed your response.
Here is my problem: the move is specifically defined as 'one square orthogonally, then one square diagonally outward.'
My assumption (possibly/apparently incorrect) is that spaces without notation are not squares, do not exist, and therefore cannot be used as part of any piece's movement.
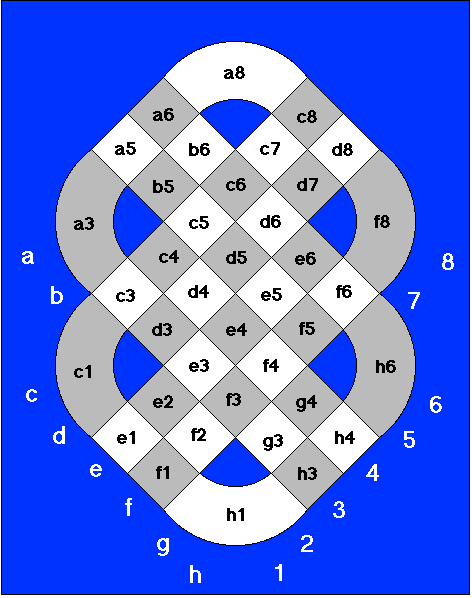
The white knight is in a8. The only spaces that appear to be orthogonally adjacent are a6 and c8. Diagonally outward from those spaces yields only b5 and d7.
I don't see a path to c6......without counting the quarter-circle empty space within a8 as orthogonally adjacent to a8. Diagonally outward from that empty space yields c6 as the destination. But I wouldn't think the empty space would be used as part of the path, at least without directly mentioning it; such as 'the knight can leap over non-existent squares.'
(If the Knight's movement was defined as one space diagonally, then one space orthogonally outward, it makes sense. The white knight starts in a8, diagonally moves to b6 or d7, and then moves orthogonally outward to one of b5, c6, or d7. The white knight would actually have two routes to c6. But the movement path of the knight is specifically defined as 1 orthogonally, then 1 diagonally outward.)
Basically, Ben Good went through the trouble of specifically defining the leaping knight's move (something I consider necessary to avoid questions on this crazy cool board) and then his example does not seem to match the defined move!
If there is a path I am missing, please show me. But the only one I see is using the non-existant quarter circle within a8.
 H. G. Muller wrote on Wed, Nov 14, 2018 07:51 AM UTC:
H. G. Muller wrote on Wed, Nov 14, 2018 07:51 AM UTC:I have no clue what you are talking about. The image on the page on which you comment doesn't show any coordinates, so I have no idea what you mean by a8, c6, etc. You must be looking at a completely different picture.
 Ben Reiniger wrote on Wed, Nov 14, 2018 03:21 PM UTC:
Ben Reiniger wrote on Wed, Nov 14, 2018 03:21 PM UTC:The board notation is available elsewhere in the game's pages: notation page
I agree that the presentation is unclear in this case. My impression is that the author just used a standard definition for knight, not recognizing the problem caused by the gaps (or assuming the diagram made it clear).
 H. G. Muller wrote on Thu, Nov 15, 2018 06:56 AM UTC:
H. G. Muller wrote on Thu, Nov 15, 2018 06:56 AM UTC:Ah, OK, he uses 45-degree rotated coordinates.
In that case, that the example that shows a Knight can move from a8 to c6 indecates that the blue areas should merely be considered inaccessible squares, i.e. like they are occupied by an uncapturable obstacle that cannot be moved by either player. But as a Knight jumps, it will ignore such obstacles, and moves as if they were normal, unoccupied board squares.
Although it is obvious what orthogonal and diagonal means in this board topology ('through sides' or 'through corners'), it is not so obvious what 'outward' means. After all, a Knight cannot make just any move that consists of an orthogonal plus a diagonal step. One could use the generalization that the diagonal step must go through a corner of the cell that was not an end-point of the side through which it entered the cell; this would allow it to go straight ahead in a triangular cell. Another generalization would be that the diagonal step can only be made throug the corner(s) farthest away from the side through which it entered; for cells with 2less than 3 or more than 4 corners this would make a difference.
Ben Reininger, thanks for linking that image. I should have done that initially.
Your comment also made me realize something I missed....if you count the knight move as 2 sq ortho/1 sq ortho to the side OR 1 sq ortho/2 sq ortho to the side.....then the knight can reach b5, c6, and d7. So yeah, it looks like he just used a standard definition (1 ortho, 1 dag outward) and then counted the squares differently for the example.
H.G. Muller, interestingly enough, I don't see a confusion with 'outward'. I just see it as 'away from starting square'. But you are correct, everything has to be defined very clearly on this crazy board.
Which now leaves us with a conumdrum.....how do knights move? Apparently we cannot use the offical way (1 ortho/1 dig outward) without contradicting the offical example.
My opinion; use both the definition and the example as offical, as the inventor probably had to spend more time and effort constructing the example than writing the definition, so it probably reflects his desires.
So, I say:
The knight can move on notated spaces, either 1 othogonally then 1 diagonally outward (outward is away from the starting square) OR 2 orthogonally then 1 orthogonally to the side, OR 1 orthogonally then 2 orthogonally to the side.
Note this does not use the inaccessable (non-notated) spaces, but I believe it can reach all squares that could be reached by using the inacessable spaces.
7 comments displayed
Permalink to the exact comments currently displayed.

How is the white knight (at the top of the board) reaching the middle square? I don't see any path to it.
This is an awesome game, btw, one of my favorites on the site.
*Edit:* I guess the empty quarter-circle shaped non-space below the white knight is counted as orthogonically adjacent to the curved space the knight is occupying, and then diagonally away. It might be better to clearly say that empty squares can be counted as a space to be leaped over. I assumed they were just non-existent.