Comments/Ratings for a Single Item

I just finished the playspace demo structure (other than a little fine-tuning and proofreading).

This game is looking more accessible all the time. This is 47"L x 35"W x 23.5"H (assuming 2" squares), which is huge as 3D setups go but still not quite unmanageable. If I make it for 1.5" squares, that becomes 35.25" x 26.25" x 17.625", which should fit on a typical dining table (even if it does take a good 15 minutes just to set up), and still leave a gap of 4.5" between the struts (which will be important if anyone moves to Face XL).

I probably could 3D print the trays, make the struts from wooden dowels or PVC pipe, print the squares on cardstock, and print the labels on some sort of decal.

This clearly cannot be played on an Interactive Diagram or in Game Courier. I don't think Jocly can handle it, either. What about Zillions of Games? (I can't purchase that one, sadly, because of a lifetime ban from Paypal which is a long and embarrassing story.) Any others?

@Fergus: Does this coordinate system work, and seem to be clear? I plan to work up a version of the playspace structure with the numeric system in any event, even if it's only an illustration and/or an experiment to show myself how easy or difficult it'd be to find a specific Face.

This clearly cannot be played on an Interactive Diagram or in Game Courier. I don't think Jocly can handle it, either. What about Zillions of Games?

Apart from multi-player games, which this is not, Game Courier can be used for any Chess variant Zillions-of-Games can be used for. So, if it can't be played on Game Courier, it can't be played on Zillions-of-Games. However, it might be doable in Game Courier if you laid out the 24 faces on a 2D surface and labeled each one.

Any others?

If you want to create a 3D playing area, Steam might be useful, but I don't know if it can handle rule enforcement. Since you already have experience with creating 3D pieces for printing, you might have an easier time developing for Steam than I would have. For CV programs and systems with 2D displays, nothing is more configurable than Game Courier.

Does this coordinate system work, and seem to be clear?

It looks horribly confusing, but I'll see if I can make more sense of it tomorrow when it isn't so late.

Apart from multi-player games, which this is not, Game Courier can be used for any Chess variant Zillions-of-Games can be used for. So, if it can't be played on Game Courier, it can't be played on Zillions-of-Games. However, it might be doable in Game Courier if you laid out the 24 faces on a 2D surface and labeled each one.

That 2D layout is actually a task to be done anyway, if only for people who don't want to set up a 3D structure (and, presumably, and the extra table space).

I suspect, though, that for GC I'd have to turn the Open Faces (NW/NE/SW/SE) 45 degrees.

It looks horribly confusing, but I'll see if I can make more sense of it tomorrow when it isn't so late.

It may help to consult the playspace picture, too. I might even add a picture of it from White's perspective, where the four cardinal and four semi-cardinal directions are laid out as they would appear on a map, and the High faces are directly above their Low counterparts.

It remains horribly confusing. One thing you are missing is a big picture perspective on how everything fits together. The method I described, being based solely on the geometry of the 2D representation of a tesseract, has the big picture perspective built into it.

Its rules for adjacency are as follows:

1. If one face is on the inner cube, and one is on the outer cube, they are not adjacent. So, for any x and any y, 0x is never adjacent to yy.
2. If two different faces are on the inner cube or on the outer cube, they are adjacent if they are not on opposite sides of the cube. So, for any x, 0x or xx is adjacent to others of the same pattern except for pairs with the digits 1 and 6, 2 and 5, or 3 and 4.
3. Otherwise, two faces are adjacent if they share a digit in common.

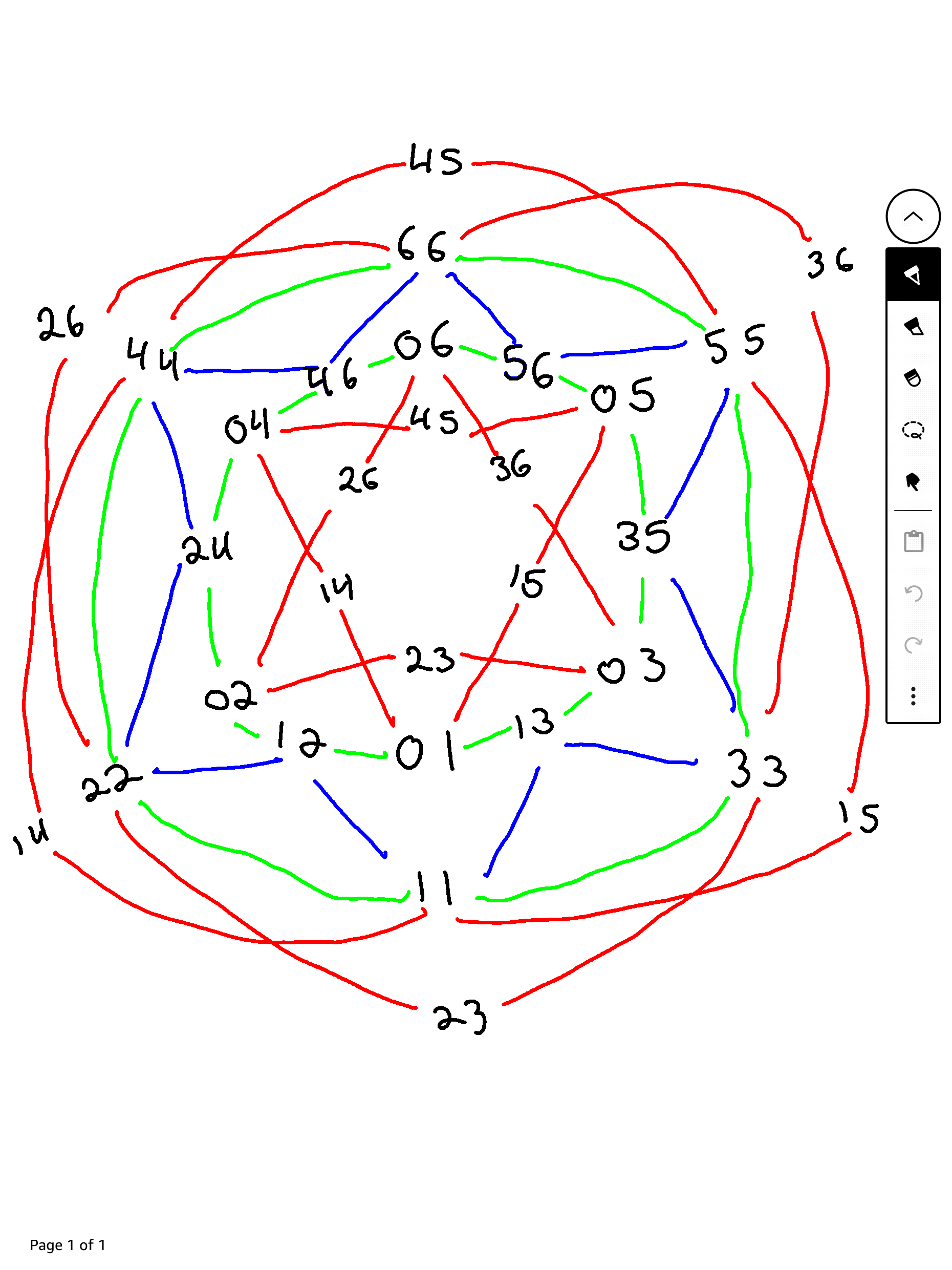
Here is an illustration of it that I drew on my Kindle Scribe this morning. Each face has lines connecting it to other faces. If there is a line between them, or there are two lines between them on the same path, then they share an edge in the tesseract. From the inside out, the paths are a star of David, a circle connecting faces of the inner cube with some neighboring faces, the outline of a star of David, a larger circle connecting faces of the outer cube, and two curved triangular shapes that interlock like a star of David. Most faces appear only once, but to avoid crowding of the diagram, six are repeated along the innermost and outermost paths. The innermost one connects them with faces of the inner cube, and the outermost one connects them with faces of the outer cube.

I'll endeavor, this week, to set up my illos (and description) to match what you're describing.

Interesting switch: while I understand your description, I find the diagram confusing. :)

Interesting switch: while I understand your description, I find the diagram confusing. :)

It was hand drawn in black and white. I have now replaced it with a colored version that uses red, green, and blue for different paths. You may need to reload it to see it. Now that I have the basic idea down, I might try doing something with more precision with a graphics program.

The colors do help. I still have yet to see if the structure shows a clear pattern for the playspace, though.

I'm also a bit resistant to setting up White on 01 and Black on 66; there's no symmetry there.

I think it would be most straightforward to number the squares by their 4d coordinates. These would be groups of 4 numbers, where two of the numbers have the value 1-5 and identify the square in a plane, while the other two numbers are either 0 or 6, indicating the plane. You can pick 2 coordinates out of 4 in 6 ways, and each of the two could have two values, so 6 x 2 x 2 = 24 different values for the faces, each with 25 squares.

Neighbors around the edge would be easily identified: 0 borders on 1, and 5 on 6. If one of the intra-face coordinates 1 or 5 would change to 0 or 6, respectively, one of the coordinates that was already 0 or 6 would have to change to 1 or 0. You can pick which one in two ways, as there are two adjacent faces.

Tracing out diagonal paths is more tricky, but the inaccessibility of the face corners guarantees that only one of the coordinates can be 1 or 5, so changing two of the coordinates by 1 to make a diagonal step can only push one of the coordinates over the edge (to become 0 or 6), and then the same prescription applies for modifying the coordinates that already were 0 or 6.

This gives an easily programmed prescription for calculating slider trajectories.

For identifying individual squares, I was thinking to go with Face:##. In my original system, the Face would be the two- or three-letter Face code, with the rank-and-file following W to B, W to E, N to S, and H to L (just use whichever two dimensions the Face sits on, in the order on that list, in the usual notation format), like the Archbishop starting at WH:d3. With Fegus's system, it'd be the two-digit code for the face, and a two-digit code going from the highest-numbered neighbor first, and from the second-highest next, making the same Archbishop start at 01:23 (I think).

I have yet to see how any of that would work in practice, though. (Tesseracts are much trickier to work with than cubes. Cubes are dogs; tesseracts are cats.)

I worked out what was the actual problem with your diagram: not enough connections. The double-digit Faces have six each, and all the rest have four. There should be eight, two for each side of the square.

But going on your descriptions, I have these as White's and Black's starting areas.:

If I got this right, then it does have an unacceptable asymmetry: Black's connections along the inner cube are all double digits, while White has different digits on all eight of its neighbors. I don't think any other game has that level of difference between the two sides.

Actually, Hyperchess4D or whatever I'm calling it now to avoid duplicate names is essentially 2D translated to a 4D board. While most people do 4D chess as basically 2D x 2D = 4D, I went with 2D + 2D = 4D, figuring that by eliminating all the 3D and 4D diagonals, the game becomes humanly playable without computer assistance.

I've been called many things; neurotypical hasn't been one until now! :) Given the fact that roughly 1 person in 10,000,000 (a rough calculation I did a few years ago) is a prolific chess variantist, I would question the "normality" of most of the people who post here. All in all, we have to be a strange group when compared to the "average" person. Not better or worse, but significantly different. (And, fwiw, my "super power" was extreme concentration, to the extent that I did not hear people talking to me while literally standing right in front of me when I was concentrating. Age has slowed me down, but I can still do it for limited times.)

Finally, I suspect [W+F] would actually be a little easier - the 2+1/1+2 slide is always orthogonal, allowing 2 potential blocking squares, and the W+F starts orthogonally then cuts right to the chase, insteadof going that extra square. And if I weren't sitting in a hospital bed right now, I'd have more to say. Later.

This seems far more complex, as there doesn't seem to be a natural way to deduce how the faces are connected. By always sorting the intra-face coordinates last you hide the information in which of the 4 dimensions the face really extends, and need to code that information in an unnatural way in the face code. Tracing an orthogonal or diagonal becomes really easy in the natural coordinates.

I worked out what was the actual problem with your diagram: not enough connections.

I've noticed that while working on a PHP script for drawing a similar diagram.

If I got this right,

As I recall from your original description of the 1-24 system, White started on 1, and Black started on 24, which were 11 and 06 in my schema. So, White started on the outer cube, and Black started on the inner cube.

So that you could start White and Black at the extreme ends of the range, I proposed starting White on the inner cube and Black on the outer. This would make no difference to gameplay, but it would let you start White on 01 and Black on 66, which is what you have depicted here.

then it does have an unacceptable asymmetry: Black's connections along the inner cube are all double digits, while White has different digits on all eight of its neighbors.

The double digits are for the outer cube, not the inner one. Being bigger, the outer cube uses bigger numbers. I don't find the asymmetry unacceptable. I wanted the labels to clearly reflect the numbers on a die while being distinguishable. Preceding the number with 0 doesn't change its value, and preceding it with itself doesn't add an extraneous element. One alternative, though, which you may find more symmetrical, would be to use 10, 20, 30, 40, 50, and 60 instead of 11, 22, 33, 44, 55, and 66. This would be an exception to the rule of writing the lower digit first. I think this would also simplify the rules for which faces are adjacent. Two faces would be adjacent if they share only a single digit, and the two digits that are different are not on the opposite sides of a die.

One alternative, though, which you may find more symmetrical, would be to use 10, 20, 30, 40, 50, and 60 instead of 11, 22, 33, 44, 55, and 66.

Bob has already done this in the Notes, except using 7 instead of the trailing 0. I don't immediately see whether one is better for a given purpose.

I agree (though I like 0,1,a,b,c,d,e for replacing "6" with something more special), but I can also see wanting something less symmetrical.

However, I'm still concerned about the coordinates inside each face in Bob's approach, and whether it's even well-defined. The four-tuples solves that.

Bob has already done this in the Notes, except using 7 instead of the trailing 0.

I saw that already, and what I proposed is an alternative to that. Also, he used 7 for the inner cube and 0 for the outer cube, which is contrary to what I proposed.

I don't immediately see whether one is better for a given purpose.

Using 10, 20, etc. is more symmetrical with 01, 02, etc. So, if symmetry is the goal, it seems to be the better alternative.

Using 10, 20, etc. is more symmetrical with 01, 02, etc. So, if symmetry is the goal, it seems to be the better alternative.

That side's not the problem. The problem area is 12-13-14-15 vs 22-33-44-55.

One alternative, though, which you may find more symmetrical, would be to use 10, 20, 30, 40, 50, and 60 instead of 11, 22, 33, 44, 55, and 66.

That would change 22-33-44-55 to 20-30-40-50, which is much better and does reflect the other side of those diagrams. I'll give that a look on a fuller diagram later, along with how things look from the Opposing Faces. It may satisfy both sets of needs.

Being bigger, the outer cube uses bigger numbers.

It isn't actually bigger. It only appears bigger in that projection.

However, I'm still concerned about the coordinates inside each face in Bob's approach, and whether it's even well-defined.

It isn't. What I wrote earlier was mostly just musing on my thoughts so far.

It isn't actually bigger. It only appears bigger in that projection.

I know that's true for the actual tesseract, but I'm referring to the 2D representation.

Anyway, I think I have my image finished.

The inner cube is on the inner most circle, the outer cube is on the outermost circle, and the intermediate faces are in the middle circle. Each face on a circle is adjacent to its two neighbors on the circle. Lines within a circle of the same color mainly connect other points on that circle, but when a line passes through a face on another circle, it also connects that face to the face at each end of the line. So, some lines do double duty, which reduces the number of lines that go from some faces. Lines that go between two circles that are each a different color than the line just connect individual pairs of faces on the two different circles.

One alternative, though, which you may find more symmetrical, would be to use 10, 20, 30, 40, 50, and 60 instead of 11, 22, 33, 44, 55, and 66. This would be an exception to the rule of writing the lower digit first. I think this would also simplify the rules for which faces are adjacent. Two faces would be adjacent if they share only a single digit, and the two digits that are different are not on the opposite sides of a die.

I did a preliminary sketch (nothing worth posting) of the diagram with this change, taken from a different projection of a tesseract, and the elegence is very appealing. I also used the same projection for my current letter-code version, and while it's not really any less elegant it is definitely less legible.

I'll put both up tomorrow morning.

To check out how the sides really relate to each other, I decided to use a side-view projection of a tesseract rather than an end-view. Here's the bare figure:

It's basically two cubes, offset at an angle, with their corners connected by bars that are the same length as the ones that make up the cubes.

I used a different viewing angle to look at the Face codes, but here's Fergus' version as I understand it:

The changing of the double-digits to numeral-zero figures makes for a very elegant symmetry. The numbers on the cubes proper are just the same, reversed. All of the other sides have the characteristic that the first digit on one side plus the second digit on the opposite side add up to 7.

(In the diagram, I made White's Home Face white, its Territory Faces light grey, Black's Home Face black, its Territory Faces charcoal grey, and the rest medium grey.)

Contrasting that to the present system:

This one is less legible, more descriptive (once you understand what the letters stand for), and labels the Faces in relation to the players and the play area rather than just to itself and the game. The first is a minus, the second is a plus, and the third could go either way.

So, unless an editor tells me to save myself the work, I'll go ahead and switch to the number version. I may or may not keep the letter codes for the playspace structure that I eventually build, but for the basic illustration the numbers do appear to be better.

I have other things I want to get done today, but I can get a start on all that tomorrow.

The changing of the double-digits to numeral-zero figures makes for a very elegant symmetry. The numbers on the cubes proper are just the same, reversed. All of the other sides have the characteristic that the first digit on one side plus the second digit on the opposite side add up to 7.

I have just modified my image to use the multiples of 10 instead of 11. One other feature of doing this is that the designation for each of the intermediate faces is the sum of two of the faces they are intermediate between.

I also centered the numbers better, increased the font size, and put them in yellow circles for better clarity.

It looks like your diagram has the number 64 in it. Following the rule of putting the lower digit first in labels for intermediate faces, that should be 46. This has the effect of making 60 the highest number used to designate any face.

It also had 63. I've corrected both errors in my own version; I just haven't uploaded that yet.