Amoeba
Introduction
In Late November, Jim Aikin sent us the following email:
Here are two entries for your 38-square competition -- AMOEBA and CUBE+. Neither of them has been tested in play, but I tried to make them both playable. Each has a couple of variants of its own.
If anybody tries out either game, I'd appreciate receiving a copy of the game so I can study it. Also, if anybody wants to try playing either of them with me by email, I'd be happy to give it a try.
The Board
The board for Amoeba consists of 38 movable squares on an underlying 7x7 matrix of locations. The locations, using standard notation, are files (columns) a through g and ranks (rows) 1 through 7. At the start of the game, there are NO squares on the following 11 locations: a1, a2, a6, a7, c4, d4, e4, g1, g2, g6, and g7. The empty board looks like this (the empty locations are shown as dots):
. - - - - - . . - - - - - . - - - - - - - - - . . . - - - - - - - - - . - - - - - . . - - - - - .
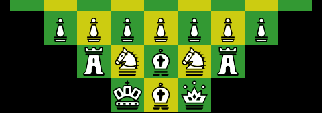
Each player begins with 10 pieces -- a king, two knights, and two rooks, plus five pawns. These are arrayed in the player's rear two rows. The arrangement is basically the familiar one: The king is in the center of the rear row (d1 or d7), flanked by the knights, with the rooks on the ends of the row and the five pawns in the second row. It looks like this:

|
|
. r n k n r . . p p p p p . - - - - - - - - - . . . - - - - - - - - - . P P P P P . . R N K N R .
|
Rules
- All pieces move in the expected manner, except that the pawns do not have the two-square option on their initial move (thus no "en passant"). There is no castling. A knight may leap over a location in which there is no square, just as if the location were a square occupied by a piece.
- The game is won by checkmate in the normal way.
- After moving a piece (and before the opponent's move), the player may, but need not, slide a single unoccupied square that is vertically or horizontally adjacent to an empty location, so that it occupies that location, leaving its former location empty. Sliding a square is optional, not required, and only one slide is permitted after each move.
- It is legal to check the opponent's king by sliding a square. Sliding may also be used to remove a check. And of course you can't slide a square in such a way as to put your own king in check.
- A player may not slide a square back into the position that it occupied just before the opponent's most recent move. At least one move must intervene in which the player either slides a different square, or does not slide a square. This prevents the board from oscillating in a static manner between two configurations.
- A stalemate that a player achieves by sliding a square so that the opponent has no legal move is considered a win, not a draw. A stalemate in which no square is slid on the final move, or in which the sliding of a square after the final move is irrelevant, is a draw.
- The king can move between two squares that are diagonally adjacent, even if there are no squares that border on both of them. The king's legal moves are shown in this diagram by x's.
- A pawn can legally capture along the same sort of diagonal.
- A pawn is promoted when it reaches the last square that exists in its column. It can be promoted to either a rook or a knight. If the square the pawn is occupying BECOMES the last square in the column due to the sliding of another square, even though the pawn itself has not moved, the pawn is promoted. Such a promotion occurs at the end of the player's turn, after the player (optionally) slides a square. Thus a pawn that becomes eligible for promotion due to the OPPONENT'S sliding a square is still a pawn during the player's move, and is promoted afterward.
- . - - - - . - - x . x - - - - . K x . - - - x . x - - - - - . - . . . - - - - . - - - - - - - -
Variants
- A square may be slid into a vacant location in the normal way, even if the square is occupied at the time by a piece (either one's own piece or the opponent's).
- A promoted pawn may become a bishop, if desired.
- The locations to which a square may be slid are not limited to a 7x7 matrix. The board can be extruded by the players arbitrarily in any direction, with the proviso that no section of it can become completely detached. (A diagonal connection is considered a legal attachment.) Note that in the normal version of the game, it IS possible for one section to become completely detached from another.
(c) 1997 Jim Aikin
Written by Jim Aikin. HTML conversion and graphic by David Howe.
This is an entry in the Contest to make a chess variant on a board with 38 squares.
WWW page created: November 30, 1997.