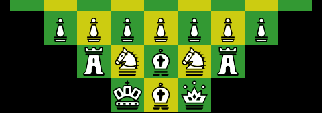
Check out Balbo's Chess, our featured variant for October, 2024.

This page is written by the game's inventor, Graeme Neatham.

Fool's Hexagonal Chess

This variant was inspired by Dave McCooey's remark about his own Hexagonal variant:

"Our goal was to create the closest hexagonal equivalent to the real game of chess as possible"

  Fool's Hexagonal Chess aspires to the same design goal and thus is intended to be:

the closest equivalent to orthodox chess of any hexagonal variant.

To judge whether or not the design goal has been met  three criteria can be applied:
  1. Faithfulness to orthodox (FIDE) rules of movement and play, with the pieces moving in an equivalent manner to their orthodox counterparts.  Styles of movement and methods of capture should thus be restricted to those found in the orthodox game;
  2. Adherence to Rule 50.
  3. Playing ambiance - the "feel" of the game should be the same.
See under Notes for further information on Rule 50 and an evaluation of the closest equivalent claim using these three criteria.

Setup

The board consists of 96 hexes in three differing colours, dark blue, light blue and white.
Iintial Array
The initial array is as illustrated here on the left.

As with orthodox chess the board consists of 8 orthogonal lines of cells, though the number of cells in each line differs. The board is placed so that the longest orthogonal line (14 hexes) runs vertically between the two players.  The White King occupies the light-blue hex at one end of the longest orthogonal, with the Black King positioned at the other end on the dark-blue hex.

If flattened the outermost 8 hexes on each side exactly match the starting position of the pieces in orthodox chess.

There is also an extra type of piece, the Fool, positioned directly in front of the Queen. The Fool moves like a King, one step in any direction to an immediately adjacent hex. This piece is discussed further under Notes.

Two further points of interest:
  • there are 32 hexes of each colour, so each Bishop covers exactly one-third of the board.
  • there is no single central hex, just as there is no single central square on the orthodox board.


Pieces

Icon
Name
Diagram
Comment
Number
pawn icon
Pawn pawn move
Moves by advancing 1 hex orthogonally. Thus, if not occupied by any piece, has a choice of 3 hexes as shown by pawn B.

Captures by advancing 1 hex along either forward facing diagonal. Thus controls 2 hexes  as demonstrated by pawn C which may capture either of the 2 rooks marked by the red dots.  Capture "en passant" of a double-moved pawn is permitted.

Has the option when moving, but not when capturing, of advancing two hexes along the same orthogonal provided the move does not finish within the opponent's part of the board.  The double-move option is illustrated by pawn A. 

Pawns promote on reaching the opponent's edge of the board.  In the diagram the 8 promotion hexes for a white pawn are marked with a green dot.
12
bishop icon
Bishop bishop move
Moves along diagonals without limit but may not jump over other pieces.
3
knight icon
Knight knight move
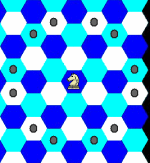
Moves 1 hex diagonally followed by 1 hex orthogonally, continuing in the same general direction 3
fool icon
Fool fool move
Like a King's normal move - 1 hex in any direction.
1
rook icon
Rook rook move
Moves along orthogonals without limit but may not jump over other pieces. 3
queen icon
Queen queen move
Combination of Rook and Bishop 1
king icon
King
king move
Moves 1 hex in any direction.
Castling is permitted under the same conditions as  for orthodox chess and is conducted in the same manner.  That is the King moves two hexes towards a Rook that stands on the same orthogonal, and this Rook is then placed on the hex over which the King has just moved. Neither King nor Rook may have previously moved.
1


Rules

The two sides are White and Black, White moving first.

Each player starts with 24 pieces. The name, number and movement of each type of piece is given in the table above.

Except where stated to the contrary, the FIDE rules of orthodox chess apply.

Notes

Rule 50

This rule arose out of a comment from Derick Peterson's Grand HexaChess -

"Comparing the movement of pieces in hexagonal variants to the movement of pieces in FIDE Chess, it is clear that the pieces should have 50% more mobility each since there are 12 directions on hexagonal grids vs. 8 directions on a square grid."

This comment refers only to piece mobility but I believe it can provide a more general guide when designing hexagonal versions of square-based games. Based on this I have formulated the rule of 50% or, more simply, Rule 50. This states -

"If a numerical representation of an attribute is possible, then this attribute in a hex-based game should exhibit a 50% increase over it's value in that game's square-based counterpart."

As a simple example orthodox chess is played on a board of 64 cells, so applying the rule of 50% leads to an hexagonal board of 96 cells.

Meta-Rules

Firstly, when looking at the FIDE rules, it must be remembered that they are, quite naturally, square-cell biased. Allowance must be made for this when applying the rules in a hex-cell environment.

For example the two orthogonals available with square-cells are, according to custom, designated as ranks and files (though curiously no such arbitrary distinction is made with the two diagonals). With hex-cells and their three orthogonals such arbitrary terms as "rank" or "file" have no relevance or real meaning, being applicable only where two orthogonals exist. So when applying FIDE rules to a hex-based chess game I consider it necessary to recast the rules, replacing square-cell only terms with an equivalent any-shaped-cell term. Thus, with this example, the terms "rank" and "file" must be replaced with "orthogonal".

Secondly, there is the matter of board shape. Again, quite naturally, FIDE rules have an unstated assumption of a regular, rectangular shaped board. Irregular and non-rectangular boards may lead to difficulties in applying the rules directly, and again I consider it necessary to recast the rules, replacing board-shape terms with an equivalent board-region based term.

To this end I have identified the following board regions for chess variants:
In a 2-player game there will be both friendly and enemy versions of these regions. In any particular variant there may be none, one, or more than one of each region. I would expect each player to at least have a Domain consisting of a Keep and Field. In orthodox chess the board regions are:
Orthodox chess has no Border and no Bailey board regions.

The result of recasting a FIDE rule to replace cell-shape and board-shape terms, I will refer to as an "equivalent meta-rule."

Evaluation of Fool's and McCooey's Hexagonal Chess

1.Faithfulness to FIDE

In most areas both variants are equally faithful to the rules of FIDE with the following exceptions -

a) Pawn movement
FIDE article 3.7.a states
"The pawn may move forward to the unoccupied square immediately in front of it on the same file"

The equivalent meta-rule is
"The pawn may move toward an enemy keep along an orthogonal to an unoccupied and immediately adjacent cell".

The application of this meta-rule results in up to 3 hexes being available to a pawn, and is applied without restriction in the Fool's variant. McCooey's variant restricts movement to a single hex by interpreting the FIDE rule to mean "pawns move without taking straight forward". This is not what the meta-rule (nor the FIDE-rule) states, but is rather a description of the result when applying the rule in a square-board, square-cell environment.

b) Castling
Castling is not permitted in McCooey's variant, whereas in the Fool's variant it is.

c) The Fool
This is the piece that lends its name to the title of the variant and may probably be the hardest aspect of the variant to justify in terms of faithfulness to orthodox chess. The idea for such a piece arose out of an attempt to adhere to Rule 50 in respect of the number of Royal, or Court, pieces. Having originally rejected the idea myself, I can understand how some will see its inclusion as instantly negating any claim of closeness to orthodox chess.

In its defence however I would point out that it does not contradict the faithfulness criteria as set out previously. It does not introduce any new style of movement nor any new method of capture. Also, although there is no orthodox piece of the same name, I think it is legitimate to see it as a second King. The new name is given to this second King to avoid confusion as to which to checkmate.

The piece itself was borrowed from Courier-Spiel, an early 19th century variant from Germany.

On balance then which is the more faithful? If my arguments for the inclusion of the second King (the Fool) are accepted then Fool's variant would seem the more faithful. If not then I am prepared to accept an honourable draw.

2.Adherence to Rule 50


Game Attribute
Orthodox Chess Value
Rule 50 Target Values
Fool's variant
McCooey's variant
Match
+/-10%
+/-20%
Value
Score
Value
Score
Cells
 64
 96
 86-106
 76-116
 96
 3
 91
 2
Pieces per side
 16
 24
 21-27
 19-29
 24
 3
 16
 0
Pawns per side
 8
 12
 10-14
 9-15
 12
 3
 7
 0
Knights per side 2
 3
 2-4
 2-4
 3
 3
 2
 2
Bishops per side 2
 3
 2-4 2-4 3
 3
 3
 3
Rooks per side 2
 3
 2-4 2-4 3
 3
 2
 2
Court Pieces per side 2
 3
 2-4 2-4 3
 3
 2
 2
Empty cells between the forces at start
 32
 48
 43-53
 38-58
 44
 2
 59
 0
Pieces per side able to make move at start
 10
 15
 13-17
 12-18
 15
 3
 10
 0
Cells protected at start
 16
 24
 21-27
 19-29
 24
 3
 21
 2
Minimum Pawn moves for Promotion
 5
 7-8
 6-9
 5-10
 7
 3
 6
 2
(Scores are assigned as: 3 for matching the target, 2 for within 10%, 1 for within 20%)

Not unexpectedly, since Rule 50 was used to guide its design, Fool's variant exhibits a much stronger adherence, scoring 97% compared to McCooey's variant which scores 45%.

3.Ambience

This is an area where only time and playing experience can make a true judgement.

I think, however, that an indication can perhaps be derived by looking at three factors:
      1. The strength of the pieces compared to the board area
      2. The importance of Pawns
      3. The importance of the centre
In an attempt to quantify these factors I have constructed the following highly speculative indices:
      1. a Strength Index - a weighted average of the cells that can be reached by each style of movement from a centre, edge and corner cell compared to the number of available cells at the start of a game. The weights applied are the number of pieces using the given style of movement.
      2. a Pawn Index - the value of the Pawns divided by the value of all the Pieces, expressed as a percentage. The value used for each piece is given under Playing Tips.
      3. a Centre Index - the ratio of the weighted cells reached by each style of movement from an edge plus a corner cell to the weighted cells reached from the centre. The weights are as in 1. with the result expressed as a percentage and subtracted from 100.
The resulting figures are -
Orthodox
McCooey's
Fool's
Strength Index
 56 46 55
Pawn Index
 21 11 22
Centre Index
 29 34 30


On balance it seems to me that Fool's variant is a closer hexagonal equivalent than McCooey's to orthodox chess, and I suspect may prove closer than any other.

But then I am the fool that designed this game and must admit to being ever-so-slightly biased!

Playing Tips

Relative Piece Values
Pawn
Knight
Bishop
Fool
Rook
Queen
Fool's variant
 1.0 2.6
 2.7
 3.3
 5.5 8.1
McCooey's variant1
 1.0
 4.1
 4.3
 --
 8.3
 12.5


1. McCooey's own estimates of the relative piece values are given as
Pawn=1 Bishop =3 Knight=4 Rook=7 Queen=10
along with the following explanation -
"...the ability to move diagonally is not as important for a piece, because each color only covers a third of the board. The result is that the Queen and Bishop are reduced in value relative to the other pieces."
What I believe was overlooked is the extreme weakness of the pawn in McCooey's variant, so that while the statement about reduced value is true with respect to non-pawns, it is not the case for the pawn itself.

This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.

By Graeme C Neatham.

Last revised by Fergus Duniho.


Web page created: 2006-11-24. Web page last updated: 2021-06-11