Check out Atomic Chess, our featured variant for November, 2024.

This page is written by the game's inventor, Florin Lupusoru.

Black Swan

Black Swans are unpredictable events that bring devastating outcomes. This game aims to mix logic with unpredictability. There have been may unsuccessful attempts to randomize the chess board, the most famous being Fisher Random Chess. However, a game called Arimaa was somewhat more successful at mixing the logic of chess with randomness, but not even this game managed to solve the problem. 

Setup

All pieces, except for the Kings, are replaced by checker pieces also called White Swans.

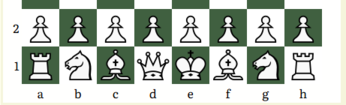
The setup looks like this:

Pieces

White Swans move and behave like Pawns, but they cannot be captured on their starting position. White Swans have their identities hidden from both players. 

Each player has a set of 20 White Swans, but only 15 of them are on the board, selected and placed in a random fashion. 

Each set of pieces has the following composition:

1) Regular pieces

2) Black Swans

Occurence:

Composition of Black Swans:

For each of the above cases pieces are selected in a random fashion according to the probability of each case. 

Rules

There is no castling. 

White Swans move and behave like Pawns, but cannot be captured on their starting position. White Swans will have to move at least one square before being fliped over and replaced by their "hidden power". Flipping over a White Swan after its first move is compulsory. 

If a White Swan turns out to be a Black Swan that will bring more that one piece on the board, one piece will remain in the position of the moved White Swan, and the other piece/pieces will be placed on nearby empty squares in their own half of the board. 

The owner of a White Swan will have to decide the placement of all the pieces on the board resulting from a Black Swan event. 

If a Pawn reaches the promotion line it can be promoted to any of the following:

If a Pawn promotes to more than one piece, one piece will replace the Pawn, while the remaining will be placed on nearby empty squares. 

If a Pawn promotes to 2 or 3 random pieces, the set of pieces has to correspond to Case 2 and Case 4 described above. 

Since White Swans are flipped over one by one, there is not the risk that the board might be jammed, considering that the occurence of Black Swans (events) is only 4 out of 20. But if that happens, the player is allowed to place the extra pieces anywhere on its half of the board on empty squares. 

If a White Swan turns out to be a Black Swan  it will be replaced straight away by the corresponding pieces, counting as a single move. 

A Black Swan (event) can no longer move and behave like a Pawn, but will be replaced by the corresponding pieces. 

Any White Swan can move two squares on the first move, like regular Pawns, even if they depart from the first rank.   

Pawns can get the two squares move on the first move only if they depart from the second rank. In this case, the en passant rule also applies. 

Notes

Players might decide the occurence of Black Swans by increassing/decreassing the number of regular pieces. 

Special Note!

People might not appreciate how great this game is until they start calculating the Setup permutations. I tried that with ChatGPT but the AI would crash every time. 

Here is my humble attempt. 

There are five possible outcomes for each player.

1) Zero Black Swans

2) One Black Swan

3) Two Black Swans

4) Three Black Swans

5) Four Black Swans

In the case of Zero Black Swans for each player we have 30 factorial = 2.65e+32.

If we calculate for the Black Swans we might get a number bigger than the total chess permutations.

This is incredible!

Also, remember that there are eight Black Swans in the game, four for each player.  

 


This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.

By Florin Lupusoru.

Last revised by Florin Lupusoru.


Web page created: 2024-01-01. Web page last updated: 2024-02-16