Wizard of Oz Nonal Chess
Wizard of Oz CVs have some few special squares comprising a contiguous Yellow Brick Road. Only when piece or Pawn situates on a YBR, the Double Move Mutator takes effect. The versions so far have been on Decimal 10x10 and Octal 8x8: 64_Squares. Shogi-size board of 9x9 here implements Nonal WoO Chess Variant.What makes this Nonal version unique are: (1) adding Falcon; (2) using 9x9; (3) interior Bishops/Scarecrows to get full coverage of board by them. Theme_Occult.
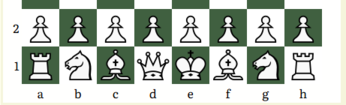
Setup
The 9x9 board is actually either the second most utilized size, or possibly only third after 10x10; and this CV is decidedly in Orthodox western style, not Japanese. Set-up is Rook-Knight-Queen-King-Bishop-Bishop-Falcon-Knight-Rook. Wizard of Oz correspondences make that 'Tinman-Lion-Witch-Wizard-Scarecrow-Scarecrow-Falcon-Lion-Tinman'. The order of the backrank array from Black's side is from file i to file a. That way the two Wizards do not face each other, and likewise for Witches. The two diagonal-moving Scarecrows each side operate on opposite square colors.As part of set-up, the standout Yellow Brick Road shall be 'c4-d5-e6-f5-g4', five spaces.
Pieces
Pieces move as usual within the equivalencies Rook/Tinman, Knight/Lion, Bishop/Scarecrow, Queen/Witch, King/Wizard. Falcon is the three-path three-stepping slider reaching the two types of squares just beyond the Knight's reach all directions. Falcon.Re-explained under Rules and in the other CVs linked, there are some different actions on the YBR squares, making the Wizard of Oz family a distinct genre involving occasional game-changing double moves.
Rules
In a logical progression, the ideal is for four Yellow Brick Road Squares on 8x8, five YBR squares on 9x9 here, and six YBR squares on 10x10. The YBR set first recommended for 9x9 is c4-d5-e6-f5-g4. When piece or Pawn stands on a YBR square, it must perform a double Move. The first part of the Move is onto another unit of either color; it cannot be onto an empty square. There is no capturing on that leg (unlike the several other two-move ideas before this one) onto the provisional or temporary square called Tornado square. The second part of what is one single Move is from its Tornado square, so defined, in continuation any direction, following a second time the rule of movement of its piece-type. Description on this way a piece moves from Yellow Brick Road is also covered in both the Octal version and the Decimal Version (See link at end).Play is normal until checkmate, just keeping in mind the special manner required on YBR five squares. In addition, Wizard as King can move along, but not off YBR without intervening Tornado square. And Witch as Queen, in contrast to all the others, does not step onto another piece at all from YBR (the Mutator applying to all but her). That is again, Witch does not move by the Double Move Mutator even from the five-cell ybr. Instead Witch/Queen must move along YBR at least one step, then either stop after the one step or continue the same radial direction any distance, including off YBR.
It becomes fairly intuitive also that Pawn has special mode off the five Road cells, one way by its non-capturing one step and another way by its capture one-step-diagonal. The latter from YBR has to be provisonally onto (tornado square) opponent piece other than King.
If there is not a piece or Pawn available from the Road to step onto, that unit requiring it cannot move at all for a while.
The exceptions are Witch and Wizard, who may be able, if not blocked, to move along the Road, or case of Witch even off the Road, according to its individual rule of movement (described already in the third paragraph of this same "Rules" section, as well as in Decimal and Octal).
Another Yellow Road square is fine to create the Tornado effect, and examples will be provided by the next WoO Chess variant.
Notes
On White's side only 'U' as Witch and two Pawns can step directly from array to a Road square with the ybr c4-d5-e6-f5-g4 and the set line-up spelled above. On Black's side with that set-up, after Pawn's move Black Falcon reaches it, as does one Pawn. In Octal Chess there are 456 possible Roads. In Nonal Chess counting every possibility there are 45*44*43*42 or 3575880, over 3.5 million. But in Nonal Chess there are desirable the same exclusions of "no adjacency" and "double adjacency." Excluding double adjacencies is tantamount to excluding any 135 degree angle and any right angle made by two orthogonals in a row. Also not wanted are Roads where a square is non-adjacent to the other four, or having two squares not contiguous the other three (no adjacency cases). Moreover, it also becomes apparent that there is even finer preference appearing that rather than a3 to a7, b3 to b7...i3 to i7 inclusive, the roads excluding all cells in a-file and i-file entirely are more elegant. Diamond patterns are not possible with five, but near-diamonds, or filament-diamonds, like e4-f5-g4-f3-g6 may as well be included as interesting and challenging. Making all such Roads between and including "end-points" or "end-rows" b- and h-files b3-b7, c3-c7...h3-h7, a 7 by 5 area square tessellation, gives roughly 2000 Yellow Brick Roads of five squares to choose from. At this point the addition of preferred Roads is not purported to be exact (as it is with Octal's 456), but there would be easily calculable some 1800 or 2000, or 2200, preliminary inspection shows in such systematic set-ups of varying Roads in and of themselves (let alone varying piece-positioned backranks for more combinations).
Potentially
thwarted thereby, and to an extent solved then for this particular size,
with so many ways to play, yet based on one the
fundamental form of Nonal Wizard of Oz having fixed Road c4-d5-e6-f5-g4 and initial position T-L-U-W-S-S-F-L-T
are: (1) Computer dominance; (2) No longer awkward spacing by dispensing of artificial Pawn three-step since the board centrality does have better utilization; (3) White first-move-advantage by trials positioning Road squares over time to effect neutrality, experimentation can progressively uncover.
Wizard_of_Oz. This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By George William Duke.
Web page created: 2015-10-06. Web page last updated: 2015-10-06