Carrousel Chess
Here's a variant I came up with that's based on Circular Chess. The game is played using a round board of 64 cells (with 4 ranks and 16 files), and the 32 standard chess pieces can be used.
A Game Courier preset page for play is available. Note that a link to Circular Chess is provided in the Notes section further below.
Setup
The setup position for Carrousel Chess looks the same as for Circular Chess:
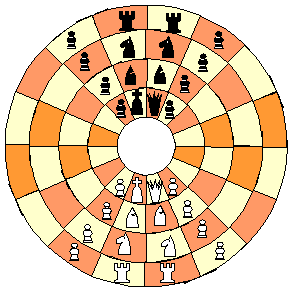
The dark orange coloured cells in the diagram are considered to be coloured that way for a decorative purpose (and also it may help in figuring out where each side's promotion ranks are), i.e. they are to be counted as dark coloured cells (that is, in the same way as the pink coloured cells are to be).
In Carrousel Chess, in comparison to Circular Chess, different movement powers and (animal) names are given to both types of minor pieces, and these (besides the round board that is used) suggested to me the name that I chose for this variant.
Pieces
In Carrousel Chess there are the 6 types of pieces, as used in standard chess, that are represented in the Setup diagram above, but there are some differences from standard chess: Three of the piece types are the Kings, Rooks and Pawns, that move much as in standard chess; see the Rules section further below for how playing on a round board affects the latter two types of pieces. The three other types of pieces in the Setup diagram have in two cases been renamed (as standard chess pieces have been in, say, the chess variant Bombalot), as their movements have been altered somewhat: The pieces represented by Knights in the setup diagram are more formally to be known in Carrousel Chess as "Jackrabbits" (Js). Jackrabbits can leap like Knights, or can leap two cells (orthogonally or diagonally) - after a known fairy chess piece type (Squirrel). The pieces represented by Bishops in the setup diagram are more formally to be known in Carrousel Chess as "Panthers" (Ts). Panthers move like Reflecting Bishops, i.e. they can reflect off cells on board edges (which are the inner and outer ranks on a round board), and continue their diagonal movement ninety degrees, and they can keep on reflecting off board edges as part of the same move; like a bishop, they can continue their movement if not compelled to stop by encountering an occupied square. Because the game is played on such a round board, a Panther can reach any cell of its own cell colour from any such cell on an empty board. Note that a link re: Reflecting Bishops is given in the Notes section further below. Queens are not renamed in Carrousel Chess, but in this game they move like Rooks or Panthers (technically, such pieces might be referred to as "Reflecting Queens", a term that may not have been used before).
Rules
Most rules for Carrousel Chess are as in standard chess, but as in Circular Chess, there are consequences to playing on a round board: Pawns move in a specific direction (away from their own king's file in the setup position), and they continue to move in that direction. Pawns promote when they reach the opposite side of the board, i.e. the nearest file on which pieces of the opponent (other than pawns) start the game. Like for Circular Chess, capturing a pawn by en passant is not allowed in Carrousel Chess. I originally wished to allow such captures, but I think that not allowing them sometimes permits desirable defensive resources, perhaps even during the opening phase of a game, given the peculiar terrain; this applies to Circular Chess itself, it seems to me. There is no castling. It is not allowed to make a move with the rook, panther or queen that ends up on the cell where the move started. For instance, consider a rook on an empty board. The rook could move entirely around the board to the place where the rook started, effectively meaning that the move didn't change the position. Such `null moves' are not allowed.
Notes
My tentative estimates for the relative values of the pieces in Carrousel Chess (for the endgame at least) are:
Pawn (P) = 1; Rook (R) = 5.5; Jackrabbit (J) = N(a Circular Chess piece not in Carrousel Chess)+N+P = 6; Panther (T) = B(a Circular Chess piece not in Carrousel Chess)*31/6 = 13 approx.; Queen (Q) = R+(T*[31-8]/31)+P = 16 approx.
Note that I estimate a Circular Chess N or B to be worth 2.5, as we'll see later. Note too that a Jackrabbit (which is not colour-bound) can reach (by short range leaping) 5 more cells than a N from any cell, and that a N can reach (by always fairly similar short range leaping) 5 cells on average itself. Also, a B can reach 6 cells from any cell on an empty board. In addition, I've applied by analogy the concept that a Q=R+B+P in chess, in treating a Jackrabbit or Carrousel Chess Queen as a kind of bi-compound piece when estimating their values (i.e. I added the value of a pawn to the sums of each of their 'component' pieces' estimated values). Plus, note a R can cover 8 cells out of the 31 that a T can reach on an empty board, if either were to be placed on the same cell.
To begin a lengthy aside, IMO a Q ought to be worth more than 8 pawns, as in chess, where a Q is often considered worth 9 pawns. I'd (tentatively) put a Q at this value in the variant Circular Chess, too. Note Q=R+B+P in value in chess, thus here meaning R+B=8, and I'll assume that applies to Circular Chess, too (a Q is often set equal to 3 minor pieces [B or N] in chess, too, but let's ignore that for now). In Circular Chess a lone R can't normally mate a lone K (but 2 Rs, or a Q, can) IMO, nor can two minor pieces mate (though N + 2 opposite-coloured Bs can) IMO, but a R and minor piece can mate IMO, so let's say for now it takes a minimum of 8 points worth of material to mate a lone Circular Chess K (not counting pawns).
If a R in Circular Chess were supposed worth 6 (how often is it worth six pawns in an endgame? - in chess, 4 pawns often beat a rook in such), and a B or N were thus supposed worth just 2, this does not quite compute, if it is realized 3 minor pieces perhaps ought to be worth more than a R (which can't normally mate like the 3 minors may). Plus, how often is a R worth minor piece + 4Ps? Or 2Rs worth Q + minor piece + P? If a R were supposed worth 5.5 (and a minor piece thus 2.5, or less than 3) then it is realized that 3 minor pieces would be worth less than 8, so that doesn't compute with the end of my previous paragraph. A rook could be set up to a value of 5.33 to avoid this problem, however (another way is to suppose that, say, 7.5 points minimum are required to mate, and I prefer that, as we'll see later). IMO, a R should be worth at least 5, since a B seems generally no stronger in Circular Chess than it is in chess. Next, note IMO a N is at least as strong as a B in Circular Chess, except note that IMO 2Ns + B may at the least have more difficulty mating a lone K than N + 2 opposite-coloured Bs, so IMO a B seems to be at least as strong as a N after taking this into consideration, thus making the pieces worth equal value.
The question I've been beating around is, is a minor piece worth less than 3 pawns in Circular Chess? Under at least some circumstances IMHO in an endgame either minor piece can deal with or at least restrain 3 enemy passed pawns, if the pawns are all going in the same direction on the round board. It's similar if 2 minor pieces faced 6 passed pawns, with exactly 3 going in either direction. This is perhaps analogous to uncommon scenarios faced in chess endgames, i.e. with passed pawns on either wing, though in all cases a lot may depend on the positions of the kings. Thus I could hazard to put a minor piece (i.e. B or N) as worth 3 pawns (it's likely more than 2, anyway), and thus a R as worth 5, in Circular Chess (I'd note one of the quirks of chess is that 3 minor pieces are often somewhat better than 2 rooks, but in Circular Chess it seems IMHO the other way around).
This matches the values many give for chess pieces. That's in spite of being contrary to the wisdom of, say, wikipedia's entry for Circular Chess (which points out K + P vs. K is almost always a win, unlike in chess, which IMHO makes up a little for other drawn basic endgames that would be basic mates in chess). For those who really dislike setting a minor piece equal to 3, I can suggest they try Q=R+B+P=9, say with R=5.5 and B(or N)=2.5, which is my favourite guess (without getting into uglier fractions) for what applies in an 'average' position, but perhaps this undervalues a Q. In any case, IMHO in Circular Chess 2 minor pieces can be worth at least a R in an endgame, if all the R side's pawns are going just one direction, and the minors side's pawns going the opposite direction, unless either of the minors is unsafe, e.g. perhaps if they are widely seperated. Also note 2Rs vs. 3 safe minor pieces + 2 pawns going in the same direction may be hard for the Rs in an endgame. On the whole the wealth of considerations based on the terrain of Circular Chess makes it understandable that there is no consensus yet on the relative values of a R, the minor pieces or a Q, as wikipedia alludes to:
https://en.wikipedia.org/wiki/Circular_chess#TheoryAs in standard chess, IMO in Carrousel Chess (or Circular Chess) a King (K) has a fighting value of 4, even though it cannot be exchanged.
In Carrousel Chess, 2 rooks or a queen still suffice to mate a lone K, and 2 opposite-coloured panthers spell (instant) mate, too. Rook + jackrabbit, or rook + panther suffice to mate, as well. IMO, also, 2 jackrabbits suffice to mate, but a jackrabbit + panther can't normally deliver mate.
To begin another aside, note that below is a link that discusses Crooked Bishops (besides Crooked Queens), which are claimed to be approx. equivalent in value to Rooks, and a Crooked Queen is there thought to be worth more than a normal Q on a 16x4 round board. I'd estimate the relative value of a Crooked Queen on such a board as R+([B*21/6]*[21-7]/21)+P = 12.33, if setting R=5.5 and B=2.5. To be clearer, on such a board I'd estimate a Crooked Bishop as worth B*21/6 (with a B moving to 6 cells from any cell on an empty board, and the average number of cells a Crooked Bishop could move to in a similar respect being [(23+1)+(15+3)]/2, or 21), or 8.75 on such a board, if setting B=2.5. Plus, note a R can always cover 7 cells out of the average of 21 that a Crooked Bishop can reach on an empty board, if either were to be placed on the same cell. Also, IMHO, a Reflecting Bishop as used in Carrousel Chess (i.e. a Panther) should indeed be generally worth more than a Crooked Bishop on the same board. That's since a Reflecting Bishop may potentially reach significantly more cells than a Crooked Bishop on the round board that is used in this game, particularly if the board becomes virtually empty, though note that a Crooked Bishop might have more scope in the opening phase of a game:
http://www.chessvariants.com/piececlopedia.dir/crooked-queen.htmlAn idea for a Carrousel Chess variant that at least some might prefer is to use Crooked Bishops and Crooked Queens. That's instead of Reflecting versions of these pieces (the reflecting diagonal moves of which might be hard to completely visualize). I'd dub this variant "Crooked Carrousel Chess" (though note this might be considered a variant that's close to being "Circular Chess, Improved" - see link further below).
For reference, here's a link to Circular Chess, as described on chessvariants.com:
http://www.chessvariants.com/shape.dir/circular.htmlAlso for reference, here's a link to Bombalot, as described on chessvariants.com:
http://www.chessvariants.com/other.dir/bombalot.htmlAgain for reference, here's a link re: Reflecting Bishops, as described on chessvariants.com:
http://www.chessvariants.com/piececlopedia.dir/reflecting-bishop.htmlHere's a link re: "Circular Chess, Improved", as described on chessvariants.com, in which Crooked Bishops & Crooked Queens are used:
http://www.chessvariants.com/shape.dir/circularchess-improved.html This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Kevin Pacey.
Last revised by Kevin Pacey.
Web page created: 2016-01-21. Web page last updated: 2016-01-21