Armies of Faith 1: The Dawn of Civilisation

The theme is different religions that have appeared and, in many cases, disappeared over the history of the Old World north of the Sahara and west of the Urals and Himalayas. My reason for confining it to that region is personal modesty - I know too little of historic religions elsewhere to feel qualified to theme variants on them. A secondary reason is that many, though not all, standard games east of said mountains have abandoned the Knight and Pawn common to all armies in this series. The overall series title, Armies of Faith, I chose to keep to a limit of 13 characters, leaving the 14th free for the number. I do not anticipate going into double figures!

Additional pieces express elements of different religions over the series, often combined with a board barring them from other religions' regions to represent religions with no tradition of proselytising beyond their founding ethnicities. They may be named...
* directly after deities - the Mesopotamian pieces here;
* after animals with whose heads deities are represented - the Egyptian pieces here and the Chaturanga Elephant (Alfil) for Ganesh in the next page's Indian-religions army;
* after types of mythical creature - particularly in the next page's European-religions army;
* after religious titles in future Judæochristian-monotheism armies (which by definition would be short of other options) - the FIDE Bishop is of course the inspiration for these;
* after real creatures related to the area continuously through changes in religion - most typically the Camel.

I progress in historical order, starting with the ancient and now dead religions of Egypt and Mesopotamia. For my knowledge of these, such as it is, I must credit the authors of Before Philosophy. Egypt grew into a single unified (if often at the expense of religious coherence) kingdom, so it is represented by a single army, represented here in Red. Mesopotamia comprised several small kingdoms throughout the time represented in this variant - Babylon, Assyria, Sumeria, Akkadia et cetera. The basic pantheon was similar but minor details such as mortal heroes varied. There are therefore rival Mesopotamian armies, represented here in Orange, Green, and Blue. The next page in this series covers later antiquity.

Setup

Level 1 includes each army's triaxial deity-based piece (the one that cannot move entirely within a single plane) with half its Knights to the right and half its Camels to the left.

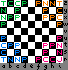
Level 2 includes each army's King and Rooks.

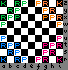
Level 3 includes each army's biaxial deity-based piece (the one that must move entirely within a single plane) and half its Knights to the left and half its Camels to the right.

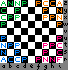
Pieces

Pieces common to both kinds of AOF1 army:
The CAMEL (C) makes 3:1:0 leaps. On an infinite cubic board it would have 24 such moves, but the moves never exceed 16 from the middle, or 12 from either other, level of a 3-level board. It is bound to half the cells. Unlike on 2d and hex-prism boards, a Camel can return to a cell in an odd number of moves, e.g. tb1-wc1-td1-wd1-wb2-tb1. There are 2 pale-cell Camels and 2 dark-cell Camels aside. Camels foreshadow both regions embracing Islam in later history, as a component of my Caliph piece.

Egypt-specific pieces:
The FALCON (F) moves to the same destinations as the Bison, but cannot leap. It makes three steps in a mixture of one orthogonal and one root-2 diagonal direction, making either one or two 45° turns but no turn of any other angle. It has three alternative routes to each destination, but is blocked from reaching that destination if every route has an intervening piece, of any army or mixture thereof. It was invented in two dimensions for Falcon Chess by George W. Duke. It has more directions to move in on this board, though fewer than it would on a board with more levels. There is 1 Falcon. It represents falcon-headed deity Horus.
The JACKAL (J) makes two steps along either the same root-3 diagonal or two root-3 diagonals that bring it to a position in an orthogonal line from the start of the move, with an optional Rook move topped and tailed by two turns of approximately 54¾° in between. On this board it can never end a move on the middle level - unless a Pawn is promoted to one there, in which case it must end its move on that level. There is 1 Jackal. It represents jackal-headed deity Anubis, and it and a hex (30° instead of 54¾° turns) counterpart are named by analogy with Tim Stiles' Wolf (which uses root-2 instead of root-3 diagonals and turns 45° instead of 54¾°).

Mesopotamia-specific pieces:
The ANU (A) is a triangulating leaper (like the Gnu). Its components are the colourswitching 4:3:0 Antelope and its colourbound dual the 7:1:0 Namel. On a cubic board of only 3 levels the only Antelope moves available are same-level ones (more levels would allow level-changing Antelope moves), but it can change level by a Namel move. Each Mesopotamian army has 1 Anu. The name is after a powerful and harsh male deity, literally meaning "sky" like his counterparts in many mythologies. Its use for this piece combines the start of Antelope with a final U for a triangulating compound by analogy to Gnu.
The NINTU (T) is the shortest-leap triaxial triangulating leaper. Its components are the colourswitching 2:2:1 Ninja and its colourbound dual the 4:1:1 Nimel. It has no same-level moves. Each Mesopotamian army has 1 Nintu. The name, literally meaning "lady of birth", is after a mother deity. Its use for this piece combines the start of Ninja with a final U for a triangulating compound by analogy to Gnu.

Rules

Pawns have an optional double-step noncapturing move along either horizontal orthogonal from the starting cell of any Pawn of the same army (including its own). Enemy Pawns (but no other piece) can immediately capture them En Passant as if they had made only the single step.

There is no Castling.

A Pawn ending a move on a column where a Knight and Camel of the

opposite

A player is Checkmated when their King is threatened by the player about to move. That player's pieces are removed from the game and the remaining players then alternate moves starting with the Checkmating one. The player delivering the third Checkmate wins. A player can also win by getting a Pawn to the far column while having a full complement of pieces to which it could be promoted there, even if 2 or all 3 enemies are uncheckmated.

Notes

This game can be played with two distinguishable pairs of identical FIDE sets - that is, each set identical to one other and distinguishable from the other two. Each player uses pieces of one colour from one pair of sets. The King, Rook, Knight, and Pawn represent themselves, and the Bishop the (similarly-bound) Camel. The Queen represents the Nintu (as the character is female) and Jackal (which like the Nintu is triaxial). The inverted Rook represents the Anu and Falcon.

Mr. Duke holds a copyright on using the Falcon in conjunction with the standard FIDE pieces on a board of 1 by 8 or a larger board containing this. Armies of Faith 1, however, has two features ensuring that it does not breach this copyright. One is that it substitutes exotic pieces for the Queen and Bishop, and the other is that no dimension exceeds 9.

The Anu's and Nintu's components are coprime oblique leapers sharing length leaps with non-coprime radial ones: the Antelope 5 like the 5:0 Quibbler; the Namel root 50 like the 5:5 Quitter; the Ninja 3 like the 3:0 Trebuchet; and the Nimel root 18 like the 3:3 Tripper. The mostly-geometrical names of leap-length-defined compounds do not suit this kind of themed variant, but for the record are Antelope+Quibbler=Fiveleaper, Namel+Quitter=Rootfiftyleaper, Ninja+Trebuchet=Threeleaper, Nimel+Tripper=Rooteighteenleaper.