Piececlopedia: Sissa
Historical notes
The sissa was invented by Carlos Cetina in the 1980s, and was first exposed to the world at large on the Chess Variants Pages in the late 1990s. The piece is named after a historic figure from the history of chess, or, as Cetina writes:Such a name is a homage, an acknowledgment, a gratitude, a tribute that I want to make and dedicate to the Grand Father of all the chess variants inventors: to the Chaturanga's inventor, according the majority opinion of the chess historians.Cetina uses the piece in four games he invented himself:
Cetina Random Chess
Sissa
Symmetric Sissa
Coherent Chess (in which it is called the knight).
Movement
A sissa moves as follows: in one turn, first, the sissa moves one or more squares like a rook or a bishop, and then the sissa moves the same number of squares like the other of the two (bishop or rook.) So, the sissa has the following options:- First, it moves a number of squares as a rook. Then it makes a corner of 45, 135, 225, or 315 degrees, and then moves the same number of squares as a bishop. All squares that are passed by must be empty, i.e., a sissa does not jump over pieces.
- First, it moves a number of squares as a bishop. Then, it makes a corner of 45, 135, 225, or 315 degrees, and then moves the same number of squares as a rook. Again, all squares passed by must be empty.
Movement diagram
In the diagram below, the White sissa can move to all the squares marked with a red circle. It can also capture the Black queen and rook.
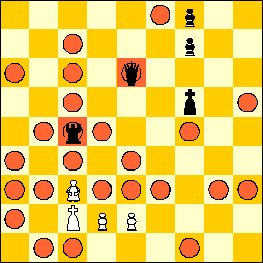
Remarks
Placed on an empty board, the sissa generally can move to any square that could be reached by a rook or a knightrider placed on the same square, although in every case it will take a different path to reach a given square than the rook or the knightrider can take. We say 'generally,' because the sissa can not always reach all the squares a rook can reach, for example, on a 9x9 board, a sissa on a1 can reach all the a-squares and all the first rank squares, but a sissa on e1 can reach e2, e3, e4, and e5, but not e6, e7 or e8 because the sides of the board block its path.The sissa has a fairly unique property of not attacking a piece that blocks its path. This is definitely a weakness on the part of the sissa, but it is somewhat compensated by the fact that it always has at least two paths to a given destination square - for example, from a1 it has two paths to g4, a1-d4-g4 and a1-d1-g4. In the case of squares that are on the same file or rank as the sissa, it may have four different paths - for example, from d4 to f4 it has four different paths, where the turning squares are d6, d2, f6, and f2.
An interesting characteristic is that it requires more pieces to block a sissa moving an odd number of squares orthogonally than it does to block a sissa moving an even number of squares orthogonally. For example, a sissa on a5 has four paths to each of b5, c5, d5, and e5. However, it takes only two pieces to block the sissa from moving to c5 or e5 (for c5, place pieees on b6 and b4 to do the blocking; for e5, place the pieces on c7 and c3), but it takes four pieces to block the sissa from moving to b5 or d5.
Investigation is still being done as to the relative value of the sissa. Thus far, the experience has been that is a piece that is somewhat weaker earlier in the game, perhaps about equal in value to a rook, since most of its potential paths are blocked, but that its value increases dramatically as the board empties, possibly to the point where it is worth a queen or more.
You can link here to a mate-in-two problem from an actual game of Symmetric Sissa won by Carlos Cetina.
This is an item in the Piececlopedia: an overview of different (fairy) chess pieces.
Written by Benjamin Good.
WWW page created: September 9, 1998. Last modified: January 15, 1999.
